ヨーロッパの孫に聞かせる
日本と世界の歴史
第１４話 ニュートンはどうして引力を発見したの
岡市敏治
ニュートンはリンゴが木から落ちるのを見て、引力を発見したんだって。地球の引力にリンゴが引っ張られたんだと学校の先生はいうの。目に見えない引力をどうしてニュートンは発見できたの。月も地球の引力に引っ張られてるんだって。だったらどうして、月は地球に落っこちてこないの？ ヒモもロープもないのに、どうして地球はリンゴや月を引っ張るの？ いったい引力はどうして発生するの？
どうして？？？
１．目と足と頭脳で地球を測った男
日本の国旗は天文学的である。それは、私たちにいちばん近い恒星・太陽を描いたものだ。日本で一番偉い神様は天照大神でこの神様も太陽の化身だ。太陽を崇めた日本人の先祖たちは、人間と宇宙とのあいだの深い関係をいくらか理解していたに違いない。
日本だけでなく、世界の国々のうち、ほぼ半数が宇宙に関係のあるものを国旗のデザインに使っている。つまり私たちはみんな、大むかしからずっと、天文学者だった。
私たち人類は、太古の昔から天を仰ぎ見て、星や星雲、惑星に思いをはせてきた。星や星座の名前も、その多くはギリシャ神話から採られたものだ。神の創造物とされてきた宇宙は、望遠鏡の発明や物理学の発達によって、次第にサイエンスとして研究されるようになった。
私たちは、観察したり観測することで、世界を拡げてきた。むかしから、地球は平らだと考えられてきた。ところが、海のはるか遠く、水平線のかなたに見える船が遠ざかるとき、下の方から次第に見えなくなっていき、やがてマストだけになって海の中に消える。太陽の高度は遠く離れた南と北とでは違う…。そういう事実から、地球が丸いのではないかと考える人たちがいた。
紀元前２２０年ごろ、エジプトのアレキサンドリアに住んでいたエラトステネス（前２７６頃～前１９４頃）はある日、パピルスの本を読んだ。
その本にはナイル川の第一の急流に近いシエネという南方の辺境駐留地の話が出ていた。そこでは、６月２１日の正午には、垂直に立てた棒には影ができないというのである。一年のうちでもっとも昼の長い夏至の日に、時刻が正午に近づくと、神殿の円形の影は次第に短くなり、正午には、消えてなくなる。そして太陽は、深い井戸の水面にも自らの姿を映している。太陽は真上にくる、というのであった。
エラトステネスは、実験する心を持っていた。彼は、アレキサンドリアで垂直に立てた棒が、６月２１日の正午に影を落とすかどうかを観察した。そして、棒は影を落とすことを発見した。
それは、ふつうの人なら見落とししまうようなことだった。棒、影、井戸の水面の反射、太陽の位置などというありきたりの日常の出来事に、どれほどの重要性があるというのか。しかし、エラトステネスは科学者であった。彼は、このような、ありきたりの出来事をじっくりと考え、世界を変えてしまった。
エラトステネは考えた。同じ時刻に、シエネの棒は影を落とさず、ずっと北のアレキサンドリアの棒はくっきりと影を落とす。それは、なぜだろうか。ここで、古代のエジプトの地図を考えてみよう。そして、同じ長さの棒をアレキサンドリアとシエネに一本ずつ垂直に立ててみよう。そして、同じ時刻に、二つの棒がともに影をまったく落とさないと想像してみよう。この場合は、地球が平らであると考えれば、きわめてたやすく理解できる。太陽は、このとき真上にあるわけだ。
しかし同じ時刻に、シエネの棒は影を落とさず、アレキサンドリアの棒ははっきりとした影を落とす。これは、いったい、どういうことなのか。
ただ一つの答えは、地球の表面が曲がっていることだ、と彼は考えた。それだけではなく、曲がり方が大きければ大きいほど、影の長さの差は大きくなる、と彼は考えた。
太陽は非常に遠く離れているので、その光が地球に届くときには、平行光線となっている。したがって、太陽光線に対して、違った角度で棒が立っていれば、影の長さに差ができる。シエネとアレキサンドリアとで生じる棒の影の長さの違いは、地球の表面にそって七度の差に相当するものだった。二本の棒が地球の中心まで伸びていると考えれば、この二本の棒は、中心のところで、七度の角度をなして交わるはずである。七度というのは、地球の全周360度の約1/50である。
エラトステネスは、ひとりの男を雇って、アレキサンドリアからシエネまでの距離を歩幅で測らせた。その距離は約800キロであった。それを50倍すれば、4万キロとなる。これが、地球の周囲の長さに違いない。 （コノ話ハ日本ノ高校「地学」ノ教科書ニ出テイルヨ）
それは、正しい答えであった。エラトステネスが使った道具は、棒と目と足と頭脳と、それから実験をする好奇心だけであった。それだけで、彼は、地球の周囲の長さを数パーセントの誤差で算出した。2200年も前の業績としては、すばらしいものであった。エラトステネスは、一つの惑星の大きさを正確に測定した最初の人間であった。
２．プトレマイオスの天動説
それから時代が３００年ほど下って（西暦１３０年ころ）同じくエジプトのアレキサンドリアにプトレマイオス（生没年不明）という天文学と地理学の学者がいた。
プトレマイオスは「地球は宇宙の中心である」と信じていた。太陽や月や、惑星や恒星は、地球の周りをめぐっているのだ。つまり天動説である。天動説はもっとも自然な考えかたであった。地球は安定しており、堅くて動かないように見えるし、天体は毎日のぼったり沈んだりしている。私たちは、それを見ることができる。
プトレマイオスはこの天動説を『アルマゲスト』という本に書いた。
大地は静止して、あらゆる天体は地球を中心にして２４時間かけて、東から西へまわるというプトレマイオスの天動説モデルは、中世の暗黒の時代には、教会が支持したこともあって、１４００年以上にわたり天文学の進歩を妨げた。
プトレマイオスの時代から、１０００年以上の時が流れ、１４世紀イタリアにルネサンスがおこった。ルネサンスはギリシャ・ローマ古典古代の自由な市民の生き方を模範とし、人間性の自由と解放を求めたヒューマニズムを基盤とする文化大革命である。ルネサンスは１５世紀から１６世紀にかけてヨーロッパ諸国にひろまっていった。
３．ルネサンス・近代科学の誕生
ルネサンスについては第６話で話したが、それをもう一度復習しよう。
そうだ、ルネサンスの合理主義精神は、１７世紀ヨーロッパに近代科学を誕生させた。
ルネサンス期の最大の成果の一つは、明快で簡潔な一貫した科学的方法が発展したことだ。科学的方法でとくに重要なのは、観察と推論（仮説）と実験で、それによって宇宙に関する理論を厳密に調べることができるようになった。この科学的方法を駆使するガリレオやニュートンによって、ヨーロッパに近代科学が誕生する。これはキリスト教出現以来の画期的な出来事で、１７世紀はヨーロッパ「科学革命」スタートの世紀となった。
４．コペルニクスの地動説
１５４３年という年は、世界史上特別な年であった。コペルニクスが「地動説」を発表したのだ。地球は太陽の周りを回っているという彼の主張は、ヨーロッパの科学に革命を引き起こした。これはヨーロッパ・キリスト教世界にとって、文字通り天も地もひっくり返るような出来事だった。
コペルニクス（1473-1543）はポーランドの天文学者である。コペルニクスは１５４３年『天球の回転について』という本を刊行した。そこには、「地球ではなく、太陽が宇宙の中心だ」とする主張（地動説）が書いてあった。
地球は惑星の一つに格下げされた。地球は太陽から３つ目の惑星で完全な円形の軌道をまわっており、且つ自転しているというものだった。発刊されたばかりのその１冊が同年５月２４日、コペルニクスの元に届けられた。その時彼は臨終の床にあり、その数時間後に息を引き取った。コペルニクスは幸いだったというべきであろう。
コペルニクスは地球の公転と自転を主張したが、その証拠を何一つ知らなかった。（その証拠は、ケプラーやニュートンの登場まで待たねばならない。）コペルニクスの次の世代のブルーノやガリレオは、地動説を信じそれを主張しただけの理由で教会側に迫害されることになる。
ジョルダーノ・ブルーノ（1548-1600）はルネサンス期イタリアの哲学者である。ナポリのドミニコ会修道士となったが、のち異端を告発されて逃亡した。ロンドンに赴いた際は、エリザベス１世の宮廷で比較的幸福な２年間を過ごした。イタリアにもどったブルーノは、コペルニクスの地動説を擁護したため、ヴェネチィアの異端審問所に告発された。ローマに護送されて７年間の尋問と拷問ののち、火刑に処された。
死に際してブルーノは「判決を受ける自分より、判決を下す諸君のほうが真理の前に恐れおののいているのではないか」と述べ、火刑の際も苦痛の声ひとつあげなかった。
イタリアは美術や文学においてルネサンスの先進地であったが、科学においてはまだ中世の暗黒の中にあった。科学者の受難は続く。
５．ガリレオ「慣性の法則」
ガリレオ・ガリレイ（1564-1642）は「ピサの斜塔」で有名なイタリアの港町ピサで生まれた。ガリレオはルネサンス期ヨーロッパの代表的な科学者で、数々の華々しい科学的成果をあげた。コペルニクスの宇宙モデル（地動説）を普及させ、振り子に関する科学的説明をした。さらに望遠鏡を改良して木星の衛星を発見した。ガリレオがはじめて真の「科学的方法」を実践し、大きく発展させたのだ。
ガリレオは、「ガリレオ・ガリレイの連続性」と呼ばれることになる次の実験（次頁右の図）をおこなった。それは相対する斜面での実験である。
振り子は左右に揺れるとき、ほぼ同じ高さまで上がることができる。ガリレオは、向き合った斜面でも、同様のことが起こるはずだと考えた。
ガリレオは、A点から初速度０で転がり始めた球が、最下点Oを通過した後、ほぼA点と同じ高さのB点まで上がることを確認した。
ここで彼は「連続性」を持ちだす。図のθを徐々に小さくしていくと、球はC、D点まで上がるはずだ。それでは、θ＝０のとき、球はどうなるか。A点と同じ高さまで上がろうとして、永遠に転がり続けるはずだ。まさにこれが、後に「慣性の法則」と呼ばれる法則の基礎になったのである。
「慣性の法則」は、力が働かなければ、物体は永遠に現在の運動形態を維持するというもの。運動する物体は、決して「何もしなければやがて止まる」のではなく、力が働かなければ、「運動形態を変えない」のだ。
この実験の事実がニュートンの引力発見につながっていく。
ガリレオとローマ・カトリック教会との衝突が起こったのは、ガリレオが７０歳近くのころで、それまでに彼はとほうもないほどたくさんの科学的業績を残していた。ガリレオが裁判沙汰に巻き込まれたのは、地動説を解説した『天文対話』を刊行したからだ。
１６３３年、ガリレオは、宗教裁判にかけられ、「地動説」は認めないという宣誓文に署名させられた。その裁判所の出口で、「それでも地球は動く」と小さくつぶやいたという話は有名である。最後の９年間、ガリレオは自宅に軟禁されて自由を奪われ、１６４２年にひっそりとこの世を去った。この同じ年、イギリスでニュートンが生まれる。
６．ケプラーの３法則
ケプラー（1571-1630）はガリレオと同時代のドイツの天文学者である。コペルニクスの地動説に感動して、天文学を志した。ケプラーは偉大な観測の天才であったデンマークの貴族ティコ・ブラーエから火星の精密、膨大な観測データを譲り受けた。
ケプラーはそのデータを解析することにより、太陽系の惑星の運動を決める簡潔な３つの法則を導きだした。この法則は、ケプラーの発見から４世紀も経った今でも天文学者や物理学者らによく利用されている。
第１法則 「惑星は、太陽を焦点のひとつとする楕円軌道上を動く」
第２法則 「惑星と太陽を結ぶ線分が単位時間に通過した時に描かれる面積は等しい」
第３法則 「惑星の公転周期の２乗は、その惑星の太陽からの平均距離の３乗に比例す
る」
T2＝kr3 T：惑星の公転周期 r：軌道の運動半径 k：比例定数
つまり、惑星は、太陽から離れていればいるほど、ゆったりと飛ぶのである。しかもそれは、「周期の2乗は、太陽からの平均距離の３乗に等しい」という数式に正確に従う。
惑星のスピートが太陽の近くでは速く、遠くでは遅くなる。これはいったい何を意味しているのだろう。どうして太陽に近づくほど惑星の動きは速くなるのだろう。
ケプラーは、太陽と惑星の間に、磁石が金属を引きつけるような力が働いているのではないかと考えた。その力の強さは太陽と惑星の距離の２乗に反比例する。近いほど強い力で引っ張るという点で、磁石とよく似ている。
しかしケプラーは、その力が何であるかということまでは突き止められなかった。その謎が解明されるためには、ニュートンの登場を待たねばならない。
７．ニュートンの登場
ニュートン（1642-1727）は歴史上もっとも偉大な天才である。彼の業績は膨大だ。物理学では万有引力の法則を、数学では微積分法をつくりあげ、神学・錬金術そのほか多くの分野でもいかんなく才能を発揮した。ニュートンのおかげで、ルネサンス期の科学が「現代科学」へと変貌を遂げたといっても過言ではない。
ニュートンの故郷イギリスのウールスソープという村には、「ニュートンのリンゴの木」と呼ばれる木が一本、今も残っている。
りんごはどうして地上に落ちるのか…？ ニュートンが着目したのは実はリンゴではなく「月の運動」であった。「リンゴは地面に落ちるのに、なぜ月は落ちてこないのか」ということだった。（まさに、冒頭の、君の疑問と同じ疑問をニュートンも持ったのだ。）
ニュートンはこの問いを自問自答し続けた。そして、「逆転の発想」がこの問題を解決するにいたる。「なぜ月は落ちてこないのか」ではなく、「なぜ月は地球の周りをいつまでもまわっているのか」「なぜ月は直線運動して地球から遠ざかっていかないのか」と考えたのだ。ここで先に話したガリレオの「慣性の法則」を思い出してほしい。何か力が働かなければ、物体は直線運動するはずだ。しかし実際には月はいつまでも地球のまわりをグルグル回っている。ならば、必ず月にはなにか「力」が働いているはずだ。そこでニュートンは「リンゴが地面に向かって落ちることと、月が地球の周りをまわっていることは、同じことではないか」と考えた。「一見、月は地球に落ちてこないように見える。しかしそうではない。地球のまわりを回ることこそ、月が地球に向かって落ち続けている証拠だ。その落ち続ける力が引力（重力）だ。」 ニュートンはそう考えたのだ。
月は地球のまわりを約２７日で１周する。月軌道はほぼ円で半径は３８万ｋｍ。月は地球の引力を受けて地球に引っ張られているが、同時に、回転に伴う外向きの遠心力も受けている。もし引力がなければどうなるだろう。その場合、円軌道を描く必要はないので、回転に伴う遠心力もなくなり、月はただ真っ直ぐに最初の速度で地球から離れていくだろう。ということは、引力が働かずに真っ直ぐに進んだ時と比べ、引力が働いて円軌道を描いている時は、確かに月は地球のほうへ落ちているのがわかるだろう。
こうして、月は軌道上を進みながら、少し進むたびにほんのわずかだけ地球に向かって落下し、それをくり返しながら、円軌道を描いているのだ。
天体の引力（重力）に引かれて天体のまわりを円運動するということは、その天体に永遠に落下し続けることなのだ。 （９頁の左図参照）
８．万有引力の法則 Ｆ＝Ｇ×Ｍｍ／ｒ２
ニュートンは次に、「月に働いている引力の大きさ」について考えた。このとき重要になるのが「ケプラーの法則」である。ケプラーは自分の師匠であるティコ・ブラーエの長年にわたる観測データを分析し、「天体の運動に対する３つの法則」を導き出したことは先に話した通りだ。
ケプラーの第３法則「惑星の運動周期Ｔの２乗は運動半径ｒの３乗に比例する」
Ｔ２＝ｋｒ３ ｋ：比例定数
ニュートンはこのケプラー第３法則に多大な影響を受けて、次の万有引力の法則を数学的に導き出したのだ。質量Ｍと質量ｍの物体に働く万有引力Ｆは
Ｆ＝Ｇ×Ｍｍ／ｒ２ Ｇ：万有引力定数 ｒ：Ｍｍ間の距離
これは逆２乗の法則である。引力は、距離の２乗に反比例して弱くなる。もし、二つの物体の距離が２倍になれば、その二つの物体がたがいにひっぱりあう力は４分の１に弱まる。もし、二つの物体の距離が１０倍になれば、引力は１０の２乗分の１、つまり１００分の１になる。引力は、明らかに逆比例の関係にある。距離とともに弱くなるのだ。だから惑星や彗星は、太陽から遠く離れたところにいるときは、ゆっくりと進み、太陽に近づくにつれて、速く動くようになる。惑星や彗星が感じている引力は、それらが太陽から離れていればいるほど弱くなる。
惑星の運動に関するケプラーの３つの法則は、全てニュートンの万有引力の法則から数学的に導き出すことができる。ケプラーの法則は、ティコ・ブラーエの苦労に満ちた観測のデータをもとにした経験則であった。それに対して、ニュートンの法則は理論的なもので、むしろ、単純な数式をもとに、ニュートンの頭脳のみによって数学的に導き出された法則であった。
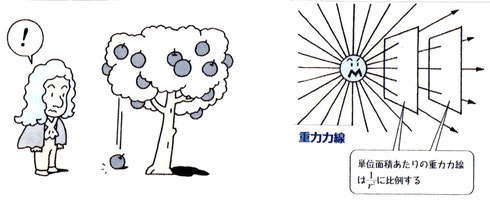
ニュートンがすごいのは、リンゴが木から落ちる運動も、惑星が太陽のまわりを回る運動も、同じ引力によるものだと気付いたところだった。地球が物体を引っ張るだけでなく、太陽は地球を引っ張っているし、地球は月を引っ張っている。だからこそ、その力のことを万有引力と呼んだ。もし天体に万有引力が働かなければ、猛スピードで動いている惑星や月はあっという間に軌道を離れ、太陽や地球から宇宙の彼方へ向かって飛び去ってしまうだろう。それを軌道につなぎ止めているのが、万有引力にほかならない。飛び去ろうとする力（遠心力）と引力が釣り合っているので、月は地球に落下することなく回転運動を続けているのだ。
「万有」こそが、ニュートンの発見の最も偉大な点である。それまで地上とは別世界だと思われていた天界が、ここで初めて理論的に統一された。リンゴが地面に落ちる現象も、月が地球のまわりを回る現象も、同じ一つの理論で説明できるようになったのだ。
とはいえ、万有引力が働く仕組みを解明したニュートンも、その「力」がどうして生じるのかまでは説明できなかった。引力が生じる仕組みについては、アインシュタインの登場を待たねばならない。
９．アインシュタイン Ｅ＝ｍｃ２
アインシュタイン（1879-1955）の相対性理論は、２０世紀物理学にとてつもない影響をおよぼし、古典物理学と現代物理学のギャップを埋める役割を果たした。この理論によって、それまで全く無名だったドイツ生まれの26才の一特許局員は、歴史上もっとも権威ある物理学者の地位をニュートンから奪いとることになった。
アインシュタインは１９０５年の特殊相対性理論で光速度不変の原理に基づいて空間と時間を「時空」に統一したが、さらにエネルギーと質量も統合した。
Ｅ＝ｍｃ２である。
これはおそらく物理学でもっとも有名な式であろう。従来は全く異質なものだと思われていたエネルギーと質量が、光速の２乗“だけ”異なる、単純に比例する物理量であることがわかったのだ。物理学の常識を覆す一大革命であった。
アインシュタインの式は、ある質量ｍは、それに光速ｃの２乗をかけただけのエネルギーＥに等しく、逆に、エネルギーＥは、それを光速ｃの２乗で割っただけの質量ｍに等しいという内容を表している。実際にはどういう意味なのだろう？
それはつまり、ごくわずかの質量でも、ｃの２乗（300,000×300,000ｋｍ／ｓ）をかければ、きわめて大きなエネルギーに換算されるということ。
例えば、1円玉1個の質量を電気エネルギーに変えることができれば、8万世帯の１ヶ月分の消費電力をまかなうことができる。だからこそ、このアインシュタインの式から、原子爆弾や原子力発電といった莫大なエネルギーを生む技術も可能になったのである。
１０．引力はどうして発生するのか
ところで、ニュートンの万有引力の法則は物体間で引力がどのように働くかを説明したが、引力が「なぜ生じるのか」ということまで説明できなかった。
遠く離れた物体同士が引きつけ合うのは実に不思議な現象だが、アインシュタインはその「不思議」に真正面から取り組んだ。その成果が、特殊相対性理論の10年後の1915年に発表された「一般相対性理論」である。
ニュートンは空間を絶対不変の「箱」のようなものと考えていた（これは私たちの常識感覚にかなっている）が、アインシュタインは相対性理論によって、空間は物理的に変化する存在（相対的なもの）であると考えた。そして、引力は空間の変化によって生じると結論づけたのである。空間そのものが歪むことで、物体同士が引っ張り合っているように見えるのだ。下図（右）を見てほしい。
その平面は、やわらかいゴムシートのような（しかし目には見えない）素材でできていると思ってほしい。その上に重い鉄の球を置くと、その部分は下にへこむ。これが、「質量で空間が曲がった」ということだ。では次に、その鉄球の近くに、もう少し質量の軽い別の鉄球を置いてみよう。平面はますます深く曲がって、２つの鉄球がそこに向かって転がり始める。つまり、どんどん２つが接近していくわけだ。そのときの速度によって、ぶつかって止まることもあれば、軽いほうが重いほうのまわりをくるくると回ることもあるだろう。いずれにしろ、曲がった平面が見えなければ、２つの物体が透明なロープで引っ張り合っているように見えるはずだ。みんな自分はまっすぐ進んでいるつもりでも、空間が曲がっているために
「落ちる」のだ。
アインシュタインはこれが引力の正体であると確信し、それを数式化した。時空と物質のすべてを統合した最終方程式が一般相対性理論の「アインシュタイン方程式」である。
式の左辺は「時空の曲がり具合」を表し、右辺は「物質の持つエネルギー」を表している。つまり式の左辺は「空間の幾何学」を、右辺はその場のエネルギーや運動量といった物質の性質を表している。この式は、物質エネルギーがどれだけ存在するかによって、時空がどのくらい曲がるのかを表している。言い方を変えれば、この方程式は「物質エネルギーがあると、その周りの空間は曲げられる（幾何学が変わってしまう）」ということを表している。
そして、エネルギーがあることによってどのくらい空間が曲げられるか、その強さを示しているのが右辺の係数８πＧ/Ｃ４である。Ｃは光速度、Ｇはニュートンの万有引力定数。ニュートンの万有引力定数Ｇがちゃんと組み込まれている。この方程式によって人類の歴史が始まって以来、初の科学的宇宙モデルを作り上げることができるようになったのだよ。
ところで、日本はこのような宇宙物理学の分野で、世界最先端を走っている。今年のノーベル物理学賞は、岐阜県飛騨の観測装置「スーパーカミオカンデ」で、宇宙からやってくるニュートリノ（素粒子）の質量を確認した梶田隆章教授が受賞した。
同じ飛騨の神岡鉱山地下に今年新設された世界初の大型重力波望遠鏡では、アインシュタインが１００年前の一般相対性理論で予言した重力波（未確認）の観測が始まるよ。重力波がキャッチできれば、宇宙誕生（ビッグバン）の謎が解明されるかもしれない。
ノーベル賞といえば、日本は２０００年以来、自然科学系（物理学、化学、医学・生理学賞）で１６人が受賞した。これはアメリカの５１人に次いで世界２位だ。ちなみにドイツのノーベル賞受賞は４位で７人だよ。 日本はニューサイエンスにおいて、ニュートンやアインシュタインを生んだヨーロッパの国々に引けを取らない貢献をしているのだ。
これで君の冒頭の疑問に対するボクのお話は終わりだ。
なにっ！？「アインシュタイン方程式」がよくわからないって？
それはボクもチンプンカンプン（nicht mehe verstand!）だ。君のパパに聞きなさい。
パパはケルン大学の物理学のprofessorなんだから。これでおしまい。
次回は『アメリカ合衆国の歴史』だよ。 （つづく） 2015.12.１